批归一化补充

批归一化的理论知识与实现在之前 CS289 的作业中已经有详细讲解了，这里谈论下对批归一化的一些理解。

1. 批归一化对梯度的隐式调节

批标准化（BN）能够稳定网络，从而允许使用远高于常规的学习率进行训练，而不会导致模型发散（即训练失败）。

我们使用 CIFAR-10 数据集做下面这个简单的实验：

# Experiment 1: High Learning Rate Sensitivity
def train_with_high_lr(model, train_loader, learning_rate, num_epochs, device, model_name):
    criterion = nn.CrossEntropyLoss()
    optimizer = optim.Adam(model.parameters(), lr=learning_rate)

    train_losses = []
    batch_losses = []  # Track per batch for detailed analysis

    model.train()
    for epoch in range(num_epochs):
        epoch_losses = []
        for batch_idx, (data, target) in enumerate(train_loader):
            data, target = data.to(device), target.to(device)
            optimizer.zero_grad()
            output = model(data)
            loss = criterion(output, target)

            # Check for NaN or infinite loss
            if torch.isnan(loss) or torch.isinf(loss):
                print(f"{model_name}: Training diverged at epoch {epoch}, batch {batch_idx}")
                return train_losses, batch_losses, True  # Diverged

            loss.backward()
            optimizer.step()

            epoch_losses.append(loss.item())
            batch_losses.append(loss.item())

        avg_loss = sum(epoch_losses) / len(epoch_losses)
        train_losses.append(avg_loss)
        print(f'{model_name} - Epoch {epoch}: Loss: {avg_loss:.4f}')

    return train_losses, batch_losses, False  # Completed successfully

# Set high learning rate for the experiment
high_learning_rate = 0.1
experiment_epochs = 8

print(f"Experiment 1: Testing with high learning rate = {high_learning_rate}")
print("="*60)

# Initialize fresh models
model_no_bn_high_lr = CNN_Without_BN().to(device)
model_bn_high_lr = CNN_With_BN().to(device)

# Train model without BN
print("\nTraining CNN without BN (High LR):")
train_losses_no_bn_high, batch_losses_no_bn_high, diverged_no_bn = train_with_high_lr(
    model_no_bn_high_lr, train_loader, high_learning_rate, experiment_epochs, device, "Without BN"
)

# Train model with BN
print("\nTraining CNN with BN (High LR):")
train_losses_bn_high, batch_losses_bn_high, diverged_bn = train_with_high_lr(
    model_bn_high_lr, train_loader, high_learning_rate, experiment_epochs, device, "With BN"
)

然后对结果绘图，得到结果如下：

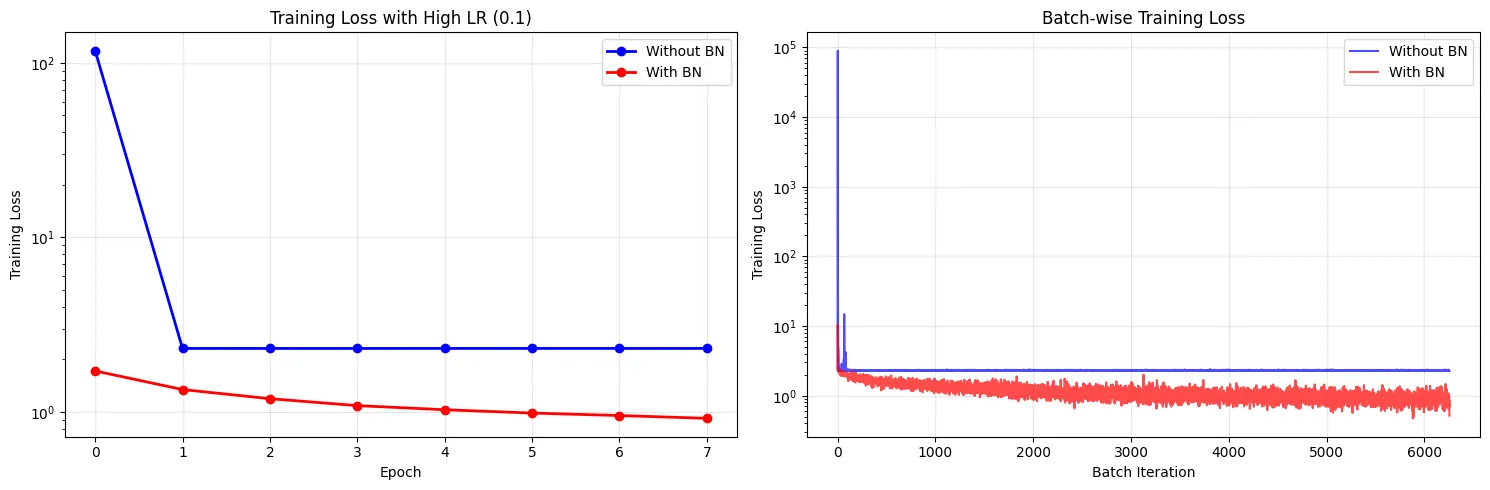
可以看到，即使在同样的高学习率下，使用批归一化的模型的训练过程依然非常稳定。损失函数曲线平滑下降，表明模型在高效、稳定地学习。

这个现象可以这么理解：BN 的作用就像是在网络的每一层都设置了一个“数值稳定器”。无论前一层的权重更新导致输入激活值变得多大或多小，BN 层都会在数据进入下一层之前，强行将其重新标准化（如拉回到均值为 0，方差为 1 的分布）。这样，学习率高导致的权重更新幅度大、激活值容易扩大的问题就被很好地抑制了。

2. mini-batch 对批归一化的影响

BN 还有一个潜在的弱点：它对 mini-batch 统计数据质量的依赖。这体现在以下几点：

标准化过程的内在随机性：BN 在训练期间本质上是一个随机过程。对于一个训练样本而言，它被标准化后的结果，完全取决于它和哪些其他的样本被随机分在了同一个 mini-batch 中。

当批量很大时，根据大数定律，这个批次的均值和方差会非常接近整个数据集的“真实”统计量。这个估计是稳定且可靠的，因此标准化过程的随机性很低，训练过程平滑。
当批量极小时，批次的均值和方差几乎完全由这几个随机样本决定。这意味着，同一个样本在不同训练步中，其被标准化的方式可能天差地别。这种剧烈的随机性正是导致“训练不稳定”的根源。

由 mini-batch 统计带来的“噪声”是一把双刃剑：

“良性正则” (Good Regularization)：当批量大小适中时（如 32,64），批次统计与全局统计之间存在温和的差异。这种“噪声”相当于在训练中对每一层的输入施加了轻微扰动。为了在这种扰动下依然能做好预测，网络必须学习到更鲁棒、泛化能力更强的特征。这正是 BN 自带正则化效果的来源。
“恶性干扰” (Bad Interference)：当批量大小过小时，这种“噪声”就不再是温和的扰动，而变成了压倒性的干扰。学习信号本身被淹没在巨大的统计噪声中，导致网络无法学习到数据中真正有用的、一致的模式，训练本身被严重干扰。

对统计估计质量的根本依赖性：BN 的有效性，根本上依赖于“批次统计量是对全局统计量的合理近似”这一假设。如果当前批次统计数据本身因批量过小而疯狂抖动，那么用这把抖动的尺子去“校准”数据，结果只会是更乱。当这个核心假设被打破时，BN 的所有优点都将无从谈起，甚至可能起反作用。

因此，选择最佳的批量大小，变成了一个需要综合考虑多方面因素的权衡过程：

大批量提供更准的统计数据，但消耗更多内存和计算时间。

大批量可能让优化器陷入更“尖锐”的局部最小值，而中小批量带来的噪声有时反而能帮助优化器找到更“平坦”、泛化能力更好的最小值。

这解释了为什么在实践中，像 32、64、128 这样的中等批量大小，会成为在统计精度、正则化强度、硬件限制和训练速度之间最常用的“最佳平衡点”。

这个的实验在 Colab 上跑一半崩了，所以只记录了观点…

3. 批处理的正则化性质

与 Dropout 相比，BN 实现了内隐的、“副作用式”的正则化。

BN 的噪声是“结构化的、基于标准化的”，而 Dropout 是“随机失活神经元”。这两种噪声有如下特点：

Dropout 的噪声：是一种“结构性”或“破坏性”的噪声。在每次训练迭代中，它以一定概率直接将神经元的输出置为零，相当于暂时“抹除”了网络中的一部分结构。这强迫网络不能过度依赖任何一个单一的神经元，必须学习到更冗余、更鲁棒的特征。它的噪声是二进制的、断开式的（一个神经元要么工作，要么不工作）。
BN 的噪声：是一种“参数化”或“统计性”的噪声。它从不“杀死”任何神经元。相反，它通过使用一个随机子集（mini-batch）的均值和方差来对激活值进行数值上的扰动。同一个样本，在不同的 batch 中，其被平移和缩放的幅度是略有不同的。这种噪声是连续的、调制式的。它保留了完整的信息流，只是给这个信息流增加了一些基于统计的“抖动”。

更进一步地，Dropout 更倾向于打破“协同适应”关系。每个神经元无法一直依赖它附近的神经元的信号，它被迫要学会从其他还在场的神经元那里寻找有用的信息（因为这些神经元有可能被 Dropout 掉）。每个神经元都被迫变得更“独立”，需要自己去学习一些更通用、更鲁棒的特征，而不是仅仅依赖于其他少数几个神经元的特定输出。

而 BN 作用于一个更宏观、更抽象的层面。它并不关心单个神经元的特征，而是使用在一个 mini-batch 上的集体统计属性 $\mu$ 、 $\sigma$ 来调整特征通道内的每一个神经元。这种机制迫使后续的网络层去学习对特征分布的整体变化不敏感的表达。网络需要回答这样一个问题：“不管这个特征通道的整体‘亮度’（均值）和‘对比度’（方差）如何轻微地随机抖动，我是否还能准确地识别出其中有用的模式？”而神经元为了在这种不确定性下依然能稳定地完成工作，就必须建立一套更鲁棒、更能抵抗宏观波动的流程，而不是依赖于某个固定不变的、精确的目标数字。