线性方程

1. 消元

$a.$ 线性方程的矩阵形式

在前面的线性代数基础中，我们提到了下面的方程：

$$\begin{aligned} x - 2y &= 1\\ 3x + 2y &= 11 \end{aligned}$$

可以写作向量的线性组合：

$$\begin{aligned} x\begin{bmatrix}1\\[4pt]3\end{bmatrix} + y\begin{bmatrix}-2\\[4pt]2\end{bmatrix} &= \begin{bmatrix}1\\[4pt]11\end{bmatrix}. \end{aligned}$$

也可以写作如下的矩阵形式：

$$A=\begin{bmatrix}1 & -2\\[4pt]3 & 2\end{bmatrix},\qquad A\begin{bmatrix}x\\[4pt]y\end{bmatrix} = \begin{bmatrix}1 & -2\\[4pt]3 & 2\end{bmatrix}\begin{bmatrix}x\\[4pt]y\end{bmatrix} = \begin{bmatrix}1\\[4pt]11\end{bmatrix}.$$

其中 $A$ 为系数矩阵。这样，我们就将线性方程转换为了矩阵形式 $A x = b$。

$b.$ 使用矩阵进行消元

考虑下面的方程：

$$\begin{aligned} 2x_1 + 4x_2 - 2x_3 &= 2\\ 4x_1 + 9x_2 - 3x_3 &= 8\\ -2x_1 - 3x_2 + 7x_3 &= 10 \end{aligned}$$

也即：

$$\begin{bmatrix} 2 & 4 & -2\\ 4 & 9 & -3\\ -2 & -3 & 7 \end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} = \begin{bmatrix}2\\8\\10\end{bmatrix}=\begin{bmatrix}{b_1}\\{b_2}\\{b_3}\end{bmatrix} = b$$

根据消元法，消元的第一步是“将第 1 个方程乘以 2，然后从第 2 个方程中减去”。并且我们希望这个过程能用一个矩阵描述，这个矩阵把我们的 $b$ 变成了 $b*{new} = E*{21}b$。

首先我们基于单位矩阵 $I$ 构造这个矩阵，因为单位矩阵相当于没有变换：$Ib=b$。然后我们让 $b'_2=b_2-2b_1$，这可以通过让 $a_{21}=-2$ 得到，于是我们得到了消元矩阵 $E_{21}$：

$$\displaystyle \begin{bmatrix}1 & 0 & 0\\ -2 & 1 & 0\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}b_1\\ b_2\\ b_3\end{bmatrix}=\begin{bmatrix}b_1\\ b_2-2b_1\\ b_3\end{bmatrix}$$

同样地，我们也可以得到其他的消元矩阵。将这个矩阵用在我们的方程上：

$$\begin{aligned} E(Ax) &= Eb\\ (EA)x &= Eb \end{aligned}$$

$c.$ 交换矩阵

在进行消元时，我们依赖于主元（即对角线上的元素）来消去其下方同一列的元素。但如果某个主元位置的元素恰好是 0，消元就无法进行下去了。这时我们就要进行行交换操作。交换矩阵 $P$ 就是用来完成这个任务的。

交换 $i$ 和 $j$ 行的矩阵 $P_{ij}$ 构造十分简单：我们从单位矩阵出发，然后交换单位矩阵的 $i$、$j$ 行即可，如：

$$P_{23} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{bmatrix}$$

令：

$$A=\begin{bmatrix}1&2&3\\[4pt]0&0&4\\[4pt]0&6&7\end{bmatrix}$$

则：

$$P_{23}A= \begin{bmatrix}1&0&0\\[4pt]0&0&1\\[4pt]0&1&0\end{bmatrix} \begin{bmatrix}1&2&3\\[4pt]0&0&4\\[4pt]0&6&7\end{bmatrix} = \begin{bmatrix}1&2&3\\[4pt]0&6&7\\[4pt]0&0&4\end{bmatrix}.$$

$d.$ 增广矩阵

消元的每一步，无论是行交换还是行倍减，都是对一整行进行的操作。这意味着，施加在 $A$ 矩阵某一行上的操作，也必须完全相同地施加在 $b$ 向量对应的分量上。于是，我们可以把 $b$ 当作 $A$ 的一个额外列，让它们形成一个更宽的矩阵，也即增广矩阵 (Augmented Matrix)。例如前面的方程可以写为：

$$[A\ b] = \left[\begin{array}{ccc|c} 2 & 4 & -2 & 2\\ 4 & 9 & -3 & 8\\ -2 & -3 & 7 & 10 \end{array}\right]$$

这样，我们的消元矩阵和变换矩阵就可以直接作用在一个矩阵上了。

2. 矩阵操作

$a.$ 基本规则

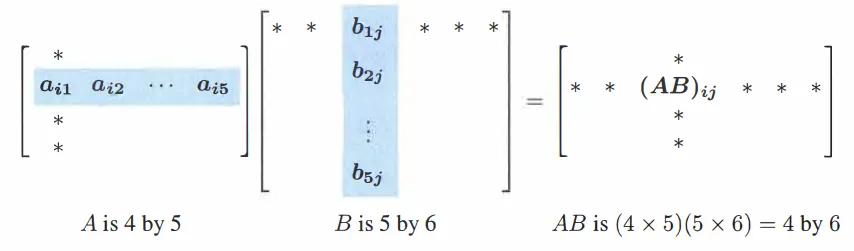
1. 维度匹配规则：一个 $m$ 行 $n$ 列的矩阵 $A\in\mathbb{R}^{m\times n}$，只能与一个 $n$ 行 $p$ 列的矩阵 $B\in\mathbb{R}^{n\times p}$ 相乘。关键在于 $A$ 的列数等于 $B$ 的行数。相乘后的结果是一个 $m$ 行 $p$ 列的矩阵 $C\in\mathbb{R}^{m\times p}$，记作：

$$(m\times n)\cdot(n\times p)=(m\times p).$$

2. 元素计算规则：结果矩阵 $C$ 中第 $i$ 行第 $j$ 列的元素 $C_{ij}$，由 $A$ 的第 $i$ 行和 $B$ 的第 $j$ 列的点积给出：

$$C_{ij}=\sum_{k=1}^{n} A_{ik}\,B_{kj}.$$

3. 结合律（Associativity）：矩阵乘法满足结合律，意味着

$$(AB)C = A(BC),$$

因此可以任选先计算哪一对乘积，结果相同。

4. 多种计算视角：

• 列视角：$AB$ 的第 $j$ 列等于 $A$ 作用于 $B$ 的第 $j$ 列：

$$(AB)_{:,j}=A\,B_{:,j}.$$

• 行视角：$AB$ 的第 $i$ 行等于 $A$ 的第 $i$ 行与 $B$ 相乘（行向量与矩阵相乘）：

$$(AB)_{i,:}=A_{i,:}\,B.$$

• 外积分解（列×行之和）：$AB$ 可以写成各列与对应行的外积之和：

$$AB=\sum_{k=1}^{n} A_{:,k}\,B_{k,:},$$

其中 $A_{:,k}$ 是第 $k$ 列，$B_{k,:}$ 是第 $k$ 行。

5. 不可交换性（Non-commutativity）：一般情况下矩阵乘法不满足交换律，即

$$AB\neq BA,$$

6. 分块乘法（Block Multiplication）：将矩阵分块后按块运算可以简化计算。若把

$$A=[A_1\ A_2],\qquad B=\begin{bmatrix}B_1\\[4pt]B_2\end{bmatrix},$$

其中块尺寸匹配，则

$$AB = A_1B_1 + A_2B_2.$$

这在处理大型矩阵或利用结构化矩阵时非常有用。

$b.$ 行视角与列视角

矩阵乘法的一般计算方法如下：第 $i$ 行第 $j$ 列的元素等于 “$A$ 的第 $i$ 行” 与 “$B$ 的第 $j$ 列” 的点积：

$$(AB)_{ij}=\sum_{k=1}^{n} A_{ik} B_{kj}.$$

而矩阵 $AB$ 的每一列，都是矩阵 $A$ 与矩阵 $B$ 相应列向量相乘的结果。进一步说，$AB$ 的每一列都是 $A$ 的所有列向量的线性组合：

$$A\,[b_1,\dots,b_p]=[Ab_1,\dots,Ab_p]$$

同样地，矩阵 $AB$ 的每一行，都是矩阵 $A$ 的相应行向量与整个矩阵 $B$ 相乘的结果。进一步说，$AB$ 的每一行都是 $B$ 的所有行向量的线性组合：

$$\text{(row }i\text{ of }A)\,[b_1,\dots,b_p] =\big[(\text{row }i\text{ of }A)b_1,\dots,(\text{row }i\text{ of }A)b_p\big] =\text{[row }i\text{ of }AB].$$

$c.$ 外积视角

矩阵乘法还可以用外积的方法分解如下：

$$AB \;=\; \sum_{k=1}^{n} A_{:,k}\,B_{k,:}$$

其中 $A_{:,k}$ 表示矩阵 $A$ 的第 $k$ 列（列向量），$B_{k,:}$ 表示矩阵 $B$ 的第 $k$ 行（行向量），它们的乘积 $A_{:,k}\,B_{k,:}$ 是一个矩阵（外积）。以下面两个矩阵为例：

$$A=\begin{bmatrix}a & b\\[4pt] c & d\end{bmatrix},\qquad B=\begin{bmatrix}E & F\\[4pt] G & H\end{bmatrix}$$

$A$ 的第 $1$ 列 与 $B$ 的第 $1$ 行 的外积：

$$A_{:,1}B_{1,:}= \begin{bmatrix}a\\[4pt]c\end{bmatrix} \begin{bmatrix}E & F\end{bmatrix} = \begin{bmatrix}aE & aF\\[4pt] cE & cF\end{bmatrix}$$

$A$ 的第 $2$ 列 与 $B$ 的第 $2$ 行 的外积：

$$A_{:,2}B_{2,:}= \begin{bmatrix}b\\[4pt]d\end{bmatrix} \begin{bmatrix}G & H\end{bmatrix} = \begin{bmatrix}bG & bH\\[4pt] dG & dH\end{bmatrix}$$

相加即得：

$$\begin{aligned} AB &= A_{:,1}B_{1,:}+A_{:,2}B_{2,:}\\[4pt] &=\begin{bmatrix}aE+bG & aF+bH\\[4pt] cE+dG & cF+dH\end{bmatrix} \end{aligned}$$

外积视角将矩阵乘法 $AB$ 分解成了 $n$ 个更简单的矩阵之和。每一个 $A_{row} B_{col}$ 都是一个“秩一矩阵”(rank-one matrix)。这种分解思想在很多高级应用中都非常重要。

$d.$ 分块

$i.$ 基本概念

矩阵的分块很简单：将矩阵用水平线和垂直线，分割成由多个子矩阵组成的网络。例如下面的矩阵：

$$\begin{bmatrix} 1 & 0 & 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 1 \end{bmatrix} = \begin{bmatrix} I & I & I\\ I & I & I \end{bmatrix},$$

分块后的矩阵比原始的 4x6 矩阵在结构上清晰得多。它能让我们从一个更高的、更宏观的视角来理解矩阵的构造，忽略掉不必要的细节。

分块矩阵也可以执行乘法操作，这是分块矩阵最有用的地方：我们可以像操作普通数字一样操作矩阵块，前提是必须满足一个关键条件：$A$ 矩阵的列切割方式，必须与 $B$ 矩阵的行切割方式完全匹配。

$b.$ 对外积表示的另一种理解

我们可以把 $A\in\mathbb{R}^{m\times n}$ 视为 $1\times n$ 的分块矩阵（每块是一列）：

$$A=\big[\;\mathrm{col}_1\;\;\mathrm{col}_2\;\cdots\;\mathrm{col}_n\;\big], \qquad \mathrm{col}_k\in\mathbb{R}^{m\times 1}.$$

然后把 $B\in\mathbb{R}^{n\times p}$ 视为 $n\times 1$ 的分块矩阵（每块是一行）：

$$B=\begin{bmatrix}\mathrm{row}_1\\[4pt]\mathrm{row}_2\\[4pt]\vdots\\[4pt]\mathrm{row}_n\end{bmatrix}, \qquad \mathrm{row}_k\in\mathbb{R}^{1\times p}.$$

此时的分块乘法结果为：

$$AB=\sum_{k=1}^{n}\mathrm{col}_k\,\mathrm{row}_k,$$

其中每一项 $\mathrm{col}_k\,\mathrm{row}_k$ 正好是一个 $m\times p$ 的外积矩阵。这说明了两种视角的等价性。

$iii.$ 分块消元与舒尔补

我们也可以对分块后的矩阵也执行前面的消元操作。普通的消元操作如下：

$$\begin{bmatrix}a & b\\[4pt] c & d\end{bmatrix} \quad\xrightarrow{\ \text{eliminate }c\ }\ \begin{aligned} &\begin{bmatrix}a & b\\[4pt] 0 & d - \dfrac{c}{a}\,b\end{bmatrix}. \end{aligned}$$

对于分块矩阵，假设

$$\begin{bmatrix}A & B\\[4pt] C & D\end{bmatrix}, \qquad A\in\mathbb{R}^{m\times m}\ \text{and is invertible}.$$

那么对其进行消元，有：

$$\begin{bmatrix}I & 0\\[4pt] -C A^{-1} & I\end{bmatrix} \begin{bmatrix}A & B\\[4pt] C & D\end{bmatrix} = \begin{bmatrix}A & B\\[4pt] 0 & D - C A^{-1} B\end{bmatrix}.$$

而右下块(又称舒尔补（Schur complement）)

$$S = D - C A^{-1} B,$$

恰好对应标量情形中的 $d - (c/a)\,b$。舒尔补在降维和解耦方面非常有用。

3. 逆矩阵

$a.$ 基本概念

假设 $A$ 是一个方阵。我们想找一个同样大小的逆矩阵 $A^{-1}$，这个矩阵乘以 $A$ 等于单位矩阵 $I$。

逆矩阵 $A^{-1}$ 的作用就是撤销 $A$ 的操作。

正式定义如下：如果存在一个矩阵 $A^{-1}$ 使得 $A^{-1}A = I$ 并且 AA⁻¹ = I，那么矩阵 A 就是可逆的 (invertible)。

关于逆矩阵的几个要点如下：

1. 逆矩阵存在的充要条件是，通过高斯消元法（允许行交换）能够得到 $n$ 个主元（对于 $n x n$ 矩阵）。这意味着消元后不会出现全零行。
2. 逆矩阵是唯一的。
3. 如果 $A$ 可逆，那么对于任何向量 $b$，方程 $Ax = b$ 都有唯一解 $x = A^{-1}b$。
4. 假设存在一个非零向量 $x$，使得 $Ax = 0$。那么 $A$ 不可能是可逆的。这是因为矩阵 $A$ 把一个非零向量 $x$ 映射到了零向量 0，而任何矩阵都无法把零向量 0 再变回原来的非零向量 $x$。换句话说，如果 $A$ 可逆，那么 $Ax = 0$ 的唯一解必然是 $x = A^{-1}0 = 0$。如果还能找到一个非零的 $x$ 满足这个方程，说明 $A$ 不可逆。

$b.$ 矩阵乘积的逆

$AB$ 可逆，当且仅当 $A$ 和 $B$ 各自都可逆（并且大小匹配）。

这个也可以从“矩阵是一种变换”的角度理解，只要这个“变换链条”中有一个部分是不可逆的，就没办法通过逆矩阵撤销整个操作。

并且 $AB$ 的逆是逆序的：

$$(AB)^{-1} = B^{-1}A^{-1}$$

$c.$ 消元矩阵的逆

这里我们特别讨论一下消元矩阵的逆，这一过程解释了 LU 分解的可行性。

假设我们有下面两个消元矩阵：

• E：从第 2 行减去 5 倍的第 1 行。
• F：从第 3 行减去 4 倍的第 2 行。

$$E=\begin{bmatrix}1&0&0\\[4pt]-5&1&0\\[4pt]0&0&1\end{bmatrix},\qquad F=\begin{bmatrix}1&0&0\\[4pt]0&1&0\\[4pt]0&-4&1\end{bmatrix}.$$

我们让它依次作用，也即计算 $FE$：

$$\begin{aligned} FE &=\begin{bmatrix}1&0&0\\[2pt]0&1&0\\[2pt]0&-4&1\end{bmatrix} \begin{bmatrix}1&0&0\\[2pt]-5&1&0\\[2pt]0&0&1\end{bmatrix} = \begin{bmatrix}1&0&0\\[2pt]-5&1&0\\[2pt]20&-4&1\end{bmatrix}. \end{aligned}$$

第三行第一列出现了一个突兀的 20，这来自交叉项：$F$ 的操作是 $\text{row}_3\leftarrow\text{row}_3-4\cdot\text{row}_2'$，而 $\text{row}_2'=\text{row}_2-5\cdot\text{row}_1$，所以 $\text{row}_3$ 收到来自 $\text{row}_1$ 的影响，产生 $(-4)\cdot(-5)=20$。

然后我们试着从最终的上三角矩阵“撤销”这些作用，也即计算 $F^{-1}E^{-1}$：

$$E^{-1}=\begin{bmatrix}1&0&0\\[4pt]5&1&0\\[4pt]0&0&1\end{bmatrix},\qquad F^{-1}=\begin{bmatrix}1&0&0\\[4pt]0&1&0\\[4pt]0&4&1\end{bmatrix}.$$ $$\begin{aligned} E^{-1}F^{-1} &=\begin{bmatrix}1&0&0\\[2pt]5&1&0\\[2pt]0&0&1\end{bmatrix} \begin{bmatrix}1&0&0\\[2pt]0&1&0\\[2pt]0&4&1\end{bmatrix} = \begin{bmatrix}1&0&0\\[2pt]5&1&0\\[2pt]0&4&1\end{bmatrix}. \end{aligned}$$

由于逆矩阵的作用是撤销矩阵操作，对于我们的消元矩阵，只需要把消元操作对应位置的符号改一下即可。

这里没有产生 20，因为逆的作用顺序是先 $F^{-1}$ 再 $E^{-1}$，$E^{-1}$ 对第二行的改变不会再传播到第三行，所以没有交叉项出现。它允许我们将所有消元步骤的乘数直接、干净地填入下三角矩阵 $L$ 中，而无需计算那些复杂的交叉项。

$d.$ 高斯——若尔当消元法

$i.$ 基本原理

高斯-若尔当 (Gauss-Jordan) 消元法的基本思路是解方程组 $AA^{-1} = I$。

设 $A^{-1}$ 的列向量为 $x_1,\dots,x_n$，单位矩阵 $I$ 的列向量为 $e_1,\dots,e_n$（例如 $e_1=[1,0,\dots,0]^T$）。则由 $AA^{-1}=I$ 得：

$$A[\,x_1\ \cdots\ x_n\,]=[\,Ax_1\ \cdots\ Ax_n\,]=[\,e_1\ \cdots\ e_n\,].$$

这等价于线性方程组：

$$\begin{aligned} A x_1 &= e_1\\ A x_2 &= e_2\\ &\vdots\\ A x_n &= e_n \end{aligned}$$

求出这 $n$ 个解向量 $x_k$ 后，即可得到 $A^{-1}$。而我们对增广矩阵

$$[\,A\mid I\,]=[\,A\mid e_1\ \cdots\ e_n\,]$$

做行简化（行初等变换），可直接得到：

$$[\,I\mid A^{-1}\,],$$

从而一次性得到 $A^{-1}$。

以下面的矩阵为例：

$$K=\begin{bmatrix}2 & -1 & 0\\-1 & 2 & -1\\0 & -1 & 2\end{bmatrix}$$

1. 构造增广矩阵 $[K\mid I]$：

$$[K\mid I]=\left[\begin{array}{ccc|ccc} 2 & -1 & 0 & 1 & 0 & 0\\[4pt] -1 & 2 & -1 & 0 & 1 & 0\\[4pt] 0 & -1 & 2 & 0 & 0 & 1 \end{array}\right]$$

2. 向下消元（得到上三角矩阵）：

• 用 $R_2\leftarrow R_2+\tfrac{1}{2}R_1$（消去第2行第1列）得

$$\left[\begin{array}{ccc|ccc} 2 & -1 & 0 & 1 & 0 & 0\\[4pt] 0 & \tfrac{3}{2} & -1 & \tfrac{1}{2} & 1 & 0\\[4pt] 0 & -1 & 2 & 0 & 0 & 1 \end{array}\right]$$

• 用 $R_3\leftarrow R_3+\tfrac{2}{3}R_2$（消去第3行第2列，注意用的是更新后的 $R_2$）得

$$\left[\begin{array}{ccc|ccc} 2 & -1 & 0 & 1 & 0 & 0\\[4pt] 0 & \tfrac{3}{2} & -1 & \tfrac{1}{2} & 1 & 0\\[4pt] 0 & 0 & \tfrac{4}{3} & \tfrac{1}{3} & \tfrac{2}{3} & 1 \end{array}\right]$$

此时左块已变为上三角矩阵 $U$。

3. 向上消元（若尔当步骤，消去上方非零元）：

• 用 $R_2\leftarrow R_2+\tfrac{3}{4}R_3$（消去 $R_2$ 的第3列）得

$$\left[\begin{array}{ccc|ccc} 2 & -1 & 0 & 1 & 0 & 0\\[4pt] 0 & \tfrac{3}{2} & 0 & \tfrac{3}{4} & \tfrac{3}{2} & \tfrac{3}{4}\\[4pt] 0 & 0 & \tfrac{4}{3} & \tfrac{1}{3} & \tfrac{2}{3} & 1 \end{array}\right]$$

• 用 $R_1\leftarrow R_1+\tfrac{2}{3}R_2$（消去 $R_1$ 的第2列，使用更新后的 $R_2$）得

$$\left[\begin{array}{ccc|ccc} 2 & 0 & 0 & \tfrac{3}{2} & 1 & \tfrac{1}{2}\\[4pt] 0 & \tfrac{3}{2} & 0 & \tfrac{3}{4} & \tfrac{3}{2} & \tfrac{3}{4}\\[4pt] 0 & 0 & \tfrac{4}{3} & \tfrac{1}{3} & \tfrac{2}{3} & 1 \end{array}\right]$$

4. 归一化，得到 $[I\mid K^{-1}]$：

• $R_1\leftarrow \tfrac{1}{2}R_1,\; R_2\leftarrow \tfrac{2}{3}R_2,\; R_3\leftarrow \tfrac{3}{4}R_3$，结果为

$$\left[\begin{array}{ccc|ccc} 1 & 0 & 0 & \tfrac{3}{4} & \tfrac{1}{2} & \tfrac{1}{4}\\[4pt] 0 & 1 & 0 & \tfrac{1}{2} & 1 & \tfrac{1}{2}\\[4pt] 0 & 0 & 1 & \tfrac{1}{4} & \tfrac{1}{2} & \tfrac{3}{4} \end{array}\right]$$

因此

$$K^{-1}=\begin{bmatrix} \tfrac{3}{4} & \tfrac{1}{2} & \tfrac{1}{4}\\[4pt] \tfrac{1}{2} & 1 & \tfrac{1}{2}\\[4pt] \tfrac{1}{4} & \tfrac{1}{2} & \tfrac{3}{4} \end{bmatrix}.$$

$e.$ 逆矩阵存在性判定

我们在前面提到了逆矩阵存在性的判定方法：一个矩阵 $A$ 存在逆矩阵 $A^{-1}$，当且仅当 $A$ 有一整套的 $n$ 个主元（对于 $n x n$ 矩阵而言，允许在消元过程中进行行交换）。通过前面的消元法方法，很容易证明这个结论。

首先我们证明：有 $n$ 个主元 $\Rightarrow$ 方阵 $A$ 可逆。

• 先证明右逆的存在：若 $A$ 在高斯——若尔当消元中有 $n$ 个主元，则对增广矩阵 $[A\mid I]$ 进行行初等变换必能化为 $[I\mid A^{-1}]$。因此由消元得到的矩阵 $A^{-1}$ 满足 $A A^{-1}=I$，即 $A^{-1}$ 是 $A$ 的一个右逆。

• 然后证明左逆的存在：消元过程等价于从左侧乘以一列行变换矩阵的乘积 $C=E_k\cdots E_2E_1$，而根据最终的变换结果，$A$ 变成了 $I$，因此 $CA=I$，$C$ 是 $A$ 的一个左逆。

然后我们证明：方阵 $A$ 可逆 $\Rightarrow$ 有 $n$ 个主元。

我们假设 $A$ 可逆但没有 $n$ 个主元（即在消元中出现至少一行全零）。消元等价于左乘一个可逆矩阵 $M$，因此消元后得到的矩阵是 $MA$，且由假设， $MA$ 存在一行全零。由于 $A$ 可逆，存在矩阵 $C$ 使得：

$$AC=I.$$

两边同时左乘 $M$ 得：

$$M(AC)=MI\quad\Longrightarrow\quad (MA)C=M.$$

考察等式两端：左侧 $(MA)C$ 若 $MA$ 存在一行全零，则 $(MA)C$ 对任意 $C$ 也必有对应的全零行。因此右侧 $M$ 必有一行全零。但这与 $M$ 可逆（$M$ 是一系列可逆矩阵的乘积）相矛盾：可逆矩阵不可能有全零行。

这个是显然的。可以使用前面的 “矩阵 $A$ 可逆，当且仅当方程 $Ax = 0$ 只有唯一的解 $x = 0$（零向量）” 这个结论。当有一行全部为 0 时，我们的方程组系统就少了一个方程，这会导致 $Ax=0$ 存在非零解。

4. LU 分解

$a.$ 基本概念

在前面，我们通过消元将 $A$ 变为了上三角矩阵：

$$E_k\cdots E_2 E_1\,A = U.$$

也即：

$$A = (E_k\cdots E_2 E_1)^{-1} U = E_1^{-1} E_2^{-1}\cdots E_k^{-1}\,U.$$

记：

$$L \;=\; E_1^{-1} E_2^{-1}\cdots E_k^{-1},$$

就得到了 $A$ 的 LU 分解：

$$A = L U$$

这个分解有一个很巧妙的地方：消元过程中的每个乘数 $l_{ij}$ 会原封不动地、直接进入由逆矩阵乘积构成的 $L$ 矩阵中，并恰好位于其 $(i, j)$ 位置。例如下面的例子：

$$E_{21}A = \begin{bmatrix}1 & 0 \\ -3 & 1\end{bmatrix}\begin{bmatrix}2 & 1 \\ 6 & 8\end{bmatrix} = \begin{bmatrix}2 & 1 \\ 0 & 5\end{bmatrix} = U$$ $$E_{21}^{-1}U = \begin{bmatrix}1 & 0 \\ 3 & 1\end{bmatrix}\begin{bmatrix}2 & 1 \\ 0 & 5\end{bmatrix} = \begin{bmatrix}2 & 1 \\ 6 & 8\end{bmatrix} = A$$

因此，我们可以如下归纳 LU 分解形式：

• $U$ (上三角矩阵): 主对角线上是主元。
• $L$ (下三角矩阵): 主对角线上全是 1，对角线下方是消元乘数 $l_{ij}$。

$b.$ 对 L 结构的解释

$L$ 结构的简单性在前面“消元”章节已经简单提过了，下面再系统整理一下：

我们考虑下面的消元步骤：先用第1行消去第2行，再用第2行消去第3行，也即 $l_{21}=\tfrac12,\;l_{32}=\tfrac23$，则

$$L=\begin{bmatrix} 1 & 0 & 0\\[4pt] \frac12 & 1 & 0\\[4pt] 0 & \frac23 & 1 \end{bmatrix},$$

注意 $L_{31}=0$，因为原始矩阵 $A$ 的第 $(3,1)$ 元已经为 $0$，不需要对第3行再用第1行消元，所以 $l_{31}=0$。

在消元过程中，我们减去的并不是原始的主元行，而是已经被更新、属于 $U$ 的行。以第 3 行为例，向下消元得到的第 3 行满足：

$$U_{3,:}=A_{3,:}-l_{31}\,U_{1,:}-l_{32}\,U_{2,:}. \tag{1}$$

将 (1) 重排，得到原始第3行关于 $U$ 行的线性组合：

$$\begin{aligned} A_{3,:} &= l_{31}\,U_{1,:} + l_{32}\,U_{2,:} + 1\cdot U_{3,:} \\ &= \begin{bmatrix} l_{31} & l_{32} & 1 \end{bmatrix} U \end{aligned}$$

对任意行 $i$ 都有类似关系，因此对整个矩阵有：

$$A = L\,U,$$

其中第 $i$ 行：

$$A_{i,:}=\sum_{k=1}^{i} l_{ik}\,U_{k,:},\qquad l_{ii}=1.$$

$c.$ LDU 分解

$A = LU$ 分解有一个“不对称”的地方：$L$ 的对角线是1，而 $U$ 的对角线是主元。我们可以很轻松地改变这一点，得到一个更“对称”的分解：我们把 $U$ 矩阵对角线上的所有主元提取出来，形成一个对角矩阵 $D$：

$$D=\operatorname{diag}(u_{11},u_{22},\dots,u_{nn}),\qquad \widehat U=D^{-1}U,$$

则 $\widehat U$ 的对角线为 $1$ 且：

$$U=D\widehat U,\qquad A=L\,U=L\,D\,\widehat U.$$

将 $\widehat U$ 记作新的 $U$，于是得到对称的 LDU 分解：

$$A = L\,D\,U$$

其中 $L$ 为单位下三角矩阵，$D$ 为对角矩阵，$U$ 为单位上三角矩阵（对角线全为 $1$）。

以下面这个矩阵为例：

$$A=\begin{bmatrix}2&1\\[4pt]6&8\end{bmatrix},\quad L=\begin{bmatrix}1&0\\[4pt]3&1\end{bmatrix},\quad U=\begin{bmatrix}2&1\\[4pt]0&5\end{bmatrix}.$$

取：

$$D=\begin{bmatrix}2&0\\[4pt]0&5\end{bmatrix},\qquad \widehat U=D^{-1}U=\begin{bmatrix}1&\tfrac12\\[4pt]0&1\end{bmatrix}.$$

于是：

$$A=L\,D\,\widehat U =\begin{bmatrix}1&0\\[4pt]3&1\end{bmatrix} \begin{bmatrix}2&0\\[4pt]0&5\end{bmatrix} \begin{bmatrix}1&\tfrac12\\[4pt]0&1\end{bmatrix}.$$

5. 转置与置换

$a.$ 转置

$i.$ 基本概念与运算

转置的概念非常简单，就是把矩阵 $A$ 的行变成 $A^T$ 的列（反之亦然）。它的运算法则如下：

1. $(A + B)^T = A^T + B^T$
2. $(AB)^T = B^TA^T$
3. $(A^{-1})^T = (A^T)^{-1}$

下面简单证明一下法则2。对向量有：

$$(Ax)^T=x^TA^T.$$

而 $B=[x_1\ x_2\ \cdots]$，则

$$AB=[Ax_1\ Ax_2\ \cdots],$$

所以 $(AB)^T$ 的行就是 $(Ax_1)^T,(Ax_2)^T,\dots$。而按上面的向量规则，

$$(Ax_j)^T=x_j^TA^T,$$

因此 $(AB)^T$ 的行正好是 $x_j^TA^T$。另一方面，$B^T$ 的行就是 $x_j^T$，于是

$ii.$ 转置的深层含义

在对转置进行更深入的讨论前，我们先引入内积与外积的新的定义：

• $\text{(Inner Product) }= x^T y$
• $\text{(Outer Product) }= x y^T$

然后我们引入下面的转置定义：对于任意的向量 $x$ 和 $y$，$A^T$ 是那个唯一能让下面这个等式成立的矩阵：

$$(Ax)^Ty = x^T(A^Ty)$$

这个式子揭示了转置的本质作用：$A^T$ 可以在内积运算中，将矩阵 $A$ 的作用对象从 $x$ 转移到 $y$ 上。

下面我们看一个具体的例子，已知：

$$A=\begin{bmatrix}-1 & 1 & 0\\[4pt]0 & -1 & 1\end{bmatrix},\qquad A^T=\begin{bmatrix}-1 & 0\\[4pt]1 & -1\\[4pt]0 & 1\end{bmatrix},$$

与向量 $x=(x_1,x_2,x_3)^T,\;y=(y_1,y_2)^T$。

1. 计算左边 $(Ax)^Ty$：

   $$\begin{aligned} Ax &= \begin{bmatrix}-1 & 1 & 0\\[4pt]0 & -1 & 1\end{bmatrix} \begin{bmatrix}x_1\\[4pt]x_2\\[4pt]x_3\end{bmatrix} =\begin{bmatrix}x_2-x_1\\[4pt]x_3-x_2\end{bmatrix},\\[6pt] (Ax)^Ty &= \begin{bmatrix}x_2-x_1 & x_3-x_2\end{bmatrix} \begin{bmatrix}y_1\\[4pt]y_2\end{bmatrix} =(x_2-x_1)y_1+(x_3-x_2)y_2\\[4pt] &=-x_1y_1+x_2(y_1-y_2)+x_3y_2. \end{aligned}$$

2. 计算右边 $x^T(A^Ty)$：

   $$\begin{aligned} A^Ty &= \begin{bmatrix}-1 & 0\\[4pt]1 & -1\\[4pt]0 & 1\end{bmatrix} \begin{bmatrix}y_1\\[4pt]y_2\end{bmatrix} =\begin{bmatrix}-y_1\\[4pt]y_1-y_2\\[4pt]y_2\end{bmatrix},\\[6pt] x^T(A^Ty) &= \begin{bmatrix}x_1 & x_2 & x_3\end{bmatrix} \begin{bmatrix}-y_1\\[4pt]y_1-y_2\\[4pt]y_2\end{bmatrix} =-x_1y_1+x_2(y_1-y_2)+x_3y_2. \end{aligned}$$

左右两边化简后相同。

$b.$ 对称矩阵

$i.$ 基本概念

如果一个矩阵的转置等于它自己，那么它就是对称矩阵。我们通常用 $S$ 来表示对称矩阵：

$$S^T=S$$

$ii.$ 对称矩阵的分解特性

对于前面的 LDU 分解：

$$S = L\,D\,U,$$

当矩阵 $S$ 为对称矩阵时，有：

$$U = L^T,$$

从而我们可以得到更为对称的分解形式：

$$S = L\,D\,L^T$$

为证明这个结论，我们对两边同时取转置：

$$S^T = U^T D^T L^T.$$

而 $S^T=S$且 $D^T=D$，于是

$$L D U = U^T D L^T.$$

通过比较两边的三角结构可以得到 $U=L^T$，于是 $S=L D L^T$。

这一分解特性是数值计算领域一个非常基本和强大的工具，它利用了矩阵的对称性来极大地提高计算和存储效率。

$c.$ 置换矩阵

$i.$ 基本概念

一个置换矩阵 $P$ 是将单位矩阵 $I$ 的行进行任意重新排序后得到的矩阵。置换矩阵有如下特征与性质：

1. 每一行、每一列都有且仅有一个 “1”，其余元素全为 “0”。
2. 任意两个置换矩阵的乘积，结果仍然是一个置换矩阵。
3. $P^{-1}=P^T$。

对性质 3 的简单证明：记 $P$ 的第 $i$ 行为 $r_i$，第 $j$ 行为 $r_j$。由于 $P$ 是置换矩阵，每一行恰有一个 1 其余为 0，且不同的行上的 1 位置互不重合，因此有：

$$r_i\cdot r_j=\begin{cases}1,&i=j,\\[4pt]0,&i\ne j.\end{cases}$$

而矩阵乘积 $(PP^T)_{ij}=r_i\cdot r_j$，由上式可得 $PP^T=I$。同理 $P^TP=I$。因此 $P^{-1}=P^T$。

$ii.$ PA = LU 分解

我们之前的 $A = LU$ 分解有一个前提：在消元过程中不需要进行行交换。但如果主元位置上出现一个 0，消元就无法进行下去，必须和下方某一行进行交换，才能得到一个非零的主元。解决这个问题只需要引入置换矩阵：

$$PA = LU$$

下面是一个具体的例子：

$$A=\begin{bmatrix}0 & 1 & 1\\[4pt]1 & 2 & 1\\[4pt]2 & 7 & 9\end{bmatrix}.$$

1. $a_{11}=0$，无法作为主元，于是用置换矩阵交换第1、2行：

$$P=\begin{bmatrix}0&1&0\\[4pt]1&0&0\\[4pt]0&0&1\end{bmatrix}, \qquad PA=\begin{bmatrix}1&2&1\\[4pt]0&1&1\\[4pt]2&7&9\end{bmatrix}.$$

2. 对 $PA$ 做标准高斯消元，可得到 $LU$ 分解（无额外行交换）：

$$L=\begin{bmatrix}1&0&0\\[4pt]0&1&0\\[4pt]2&3&1\end{bmatrix},\qquad U=\begin{bmatrix}1&2&1\\[4pt]0&1&1\\[4pt]0&0&4\end{bmatrix},$$

且

$$PA=LU.$$