Dark Dwarf Blog background

对象检测的一些基础概念

2316 words • 12 min read views
#CV #Probability #Object Detection

对象检测的一些基础概念

在介绍P-R曲线这些高级概念之前，我们先梳理一下最基本的统计指标的相关概念。

1. 核心评估指标

a.a. 准确率

准确率 (Accuracy) 的意义是：“模型总共预测对了百分之多少？”。它的定义是所有被正确分类的样本（包括正确预测为正例和正确预测为负例）占总样本数的比例：

Accuracy=TP+TNTP+TN+FP+FN\mathrm{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN}

准确率非常直观，容易理解。在**数据集均衡（正例和负例的样本数量差不多）**的情况下，可以作为一个粗略的衡量标准。但当数据非常不均衡时会产生严重误导。

假设一个数据集中，99% 的样本是负例（正常邮件），只有 1% 是正例（垃圾邮件）。一个“无脑”模型，无论什么邮件都预测为“正常邮件”，那么它的准确率会高达 99%！

b.b. 召回率

召回率 (Recall) 又称作真正率 (True Positive Rate, TPR)，它的意义是：“所有真正是正例的样本中，模型成功找出了多少？”。它的定义是被正确预测为正例的样本 (TP) 占所有实际为正例的样本 (TP + FN) 的比例：

Recall=TPTP+FN\mathrm{Recall} = \frac{TP}{TP + FN}

它衡量的是模型“抓捕”真正目标的能力，目标是宁可错抓，不可放过。当假负例 FN 的代价很高时，召回率是一个很合适的指标。

c.c. 假正率

假正率 (False Positive Rate, FPR) 的意义是：“所有真正是负例的样本中，模型错误地报了多少？”。它的定义是被错误预测为正例的样本 (FP) 占所有实际为负例的样本 (FP + TN) 的比例：

FPR=FPFP+TN\mathrm{FPR} = \frac{FP}{FP + TN}

当假正例 (FP) 的代价非常高时，这个评价指标非常有用。

d.d. 精确率

精确率 (Precision) 的意义是：“在所有被模型预测为正例的样本中，有多少是真正确的？”。它的定义是被正确预测为正例的样本 (TP) 占所有被预测为正例的样本 (TP + FP) 的比例：

Precision=TPTP+FP\mathrm{Precision} = \frac{TP}{TP + FP}

这一评价指标的使用场景和 FPR 类似，当假正例 (FP) 的代价非常高时我们也可以使用这个。

注意：精确率和召回率往往是负相关的：

  • 提高精确率：收紧标准（提高阈值），只在非常有把握时才预测为正例。这会减少 FP（误报少了），但可能导致更多 FN（漏报多了），从而降低召回率。
  • 提高召回率：放宽标准（降低阈值），尽可能多地找出所有可能的正例。这会减少 FN（漏报少了），但可能导致更多 FP（误报多了），从而降低精确率。

这一点是我们之后做平滑的理论依据。

2. 平均精确度

下面我们开始讨论平均精确度 (Average Precision, AP) 的计算和相关概念。AP 是针对单类别而言的，假设我们在计算“猫”这个类别的 AP。

a.a. 具体计算过程

假设我们获取了一系列预测结果、找到了10个可能是“猫”的物体。每个预测结果包含：

  • 预测框的位置。
  • 预测的类别（这里都是“猫”）。
  • 置信度 (Confidence Score)：模型认为这个预测是“猫”的概率，如0.98, 0.95, 0.88等

首先，我们需要将这10个预测结果从高到低按置信度排序。这是非常关键的一步。

然后我们从上到下，逐个评估每个预测、计算它的 Precision 和 Recall。假设数据集中总共有5只真实的猫（TP+FN = 5），我们可以得到如下表格：

排名置信度评估 (与真实框IoU>0.5?)TP/FP累积TP累积FP精确率 (Precision)召回率 (Recall)
10.99是TP101/1 = 1.01/5 = 0.2
20.95是TP202/2 = 1.02/5 = 0.4
30.88否 (IoU太低或重复检测)FP212/3 ≈ 0.672/5 = 0.4
40.85是TP313/4 = 0.753/5 = 0.6
50.76是TP414/5 = 0.84/5 = 0.8
60.71否FP424/6 ≈ 0.674/5 = 0.8
70.63是TP525/7 ≈ 0.715/5 = 1.0
80.55否FP535/8 ≈ 0.625/5 = 1.0
90.49否FP545/9 ≈ 0.565/5 = 1.0
100.42否FP555/10 = 0.55/5 = 1.0

可以得到如下的计算公式：

Precision=cumTPcumTP+cumFP=cumTPrankRecall=cumTPNpos=cumTP5\begin{aligned} \mathrm{Precision} &= \frac{\mathrm{cumTP}}{\mathrm{cumTP} + \mathrm{cumFP}} = \frac{\mathrm{cumTP}}{\mathrm{rank}} \\ \mathrm{Recall} &= \frac{\mathrm{cumTP}}{N_{\text{pos}}} = \frac{\mathrm{cumTP}}{5} \end{aligned}

在计算 AP 的表格中，我们不是孤立地看每一个预测，而是在一个累积的视角下。当我们评估到当前排名”为 k的预测时，我们实际上是在评估从排名 1 到排名 k 的所有 k 个预测的整体表现。因此 Precision 的计算的分母为 rank。

然后，我们以召回率 (Recall) 为横轴，精确率 (Precision) 为纵轴，将上表中的点（(0.2, 1.0), (0.4, 1.0), (0.4, 0.67), (0.6, 0.75), …）画出来，就得到了一条 P-R 曲线：

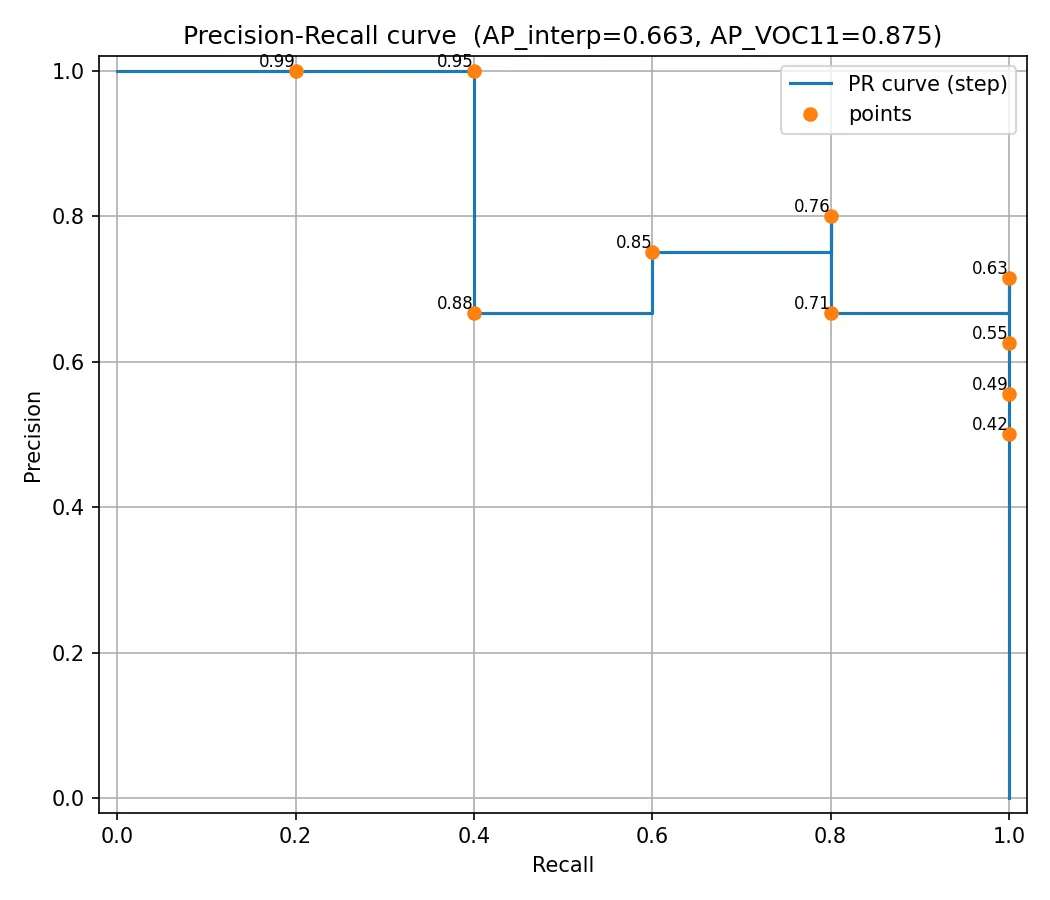
alt text

然后，AP 就是这条 P-R 曲线下方的面积。这个面积越大，说明模型在各个召回率水平上都能保持较高的精确率，性能越好。

b.b. mAP

有了 AP 的计算，mAP (mean Average Precision) 的计算就非常简单了：我们按照上面的方法计算出每个类别的 AP，然后把所有类别的 AP 加上来求平均即可。

c.c. P-R 曲线的平滑

前面的P-R 曲线有一个很明显的特征：它呈现锯齿状、而不是直接的负相关。这是不符合直觉的，于是在计算AP之前，我们会先对曲线进行平滑处理。平滑的规则如下：

  • 对于每一个召回率水平，我们都用其右侧所有召回率水平中出现过的最大精确率值来替换当前的精确率值。

也即：

Pinterp(r)=max⁡r′≥rp(r′)P_{\mathrm{interp}}(r) = \max_{r' \ge r} p(r')

前面的猫的表格平滑后的值如下：

排名评估召回率原始精确率平滑后的精确率 (P_interp)计算逻辑
1TP0.21.01.0从当前行及以后所有行的“原始精确率”中取最大值（max(1.0, 1.0, 0.67…) = 1.0）
2TP0.41.01.0从当前行及以后所有行的“原始精确率”中取最大值（max(1.0, 0.67, 0.75…) = 1.0）
3FP0.40.670.8从当前行及以后所有行的“原始精确率”中取最大值（max(0.67, 0.75, 0.8…) = 0.8）
4TP0.60.750.8从当前行及以后所有行的“原始精确率”中取最大值（max(0.75, 0.8, 0.67…) = 0.8）
5TP0.80.80.8从当前行及以后所有行的“原始精确率”中取最大值（max(0.8, 0.67, 0.71…) = 0.8）
6FP0.80.670.71从当前行及以后所有行的“原始精确率”中取最大值（max(0.67, 0.71, 0.62…) = 0.71）
7TP1.00.710.71从当前行及以后所有行的“原始精确率”中取最大值（max(0.71, 0.62, 0.56…) = 0.71）
………………

平滑后的 P-R 曲线如下：

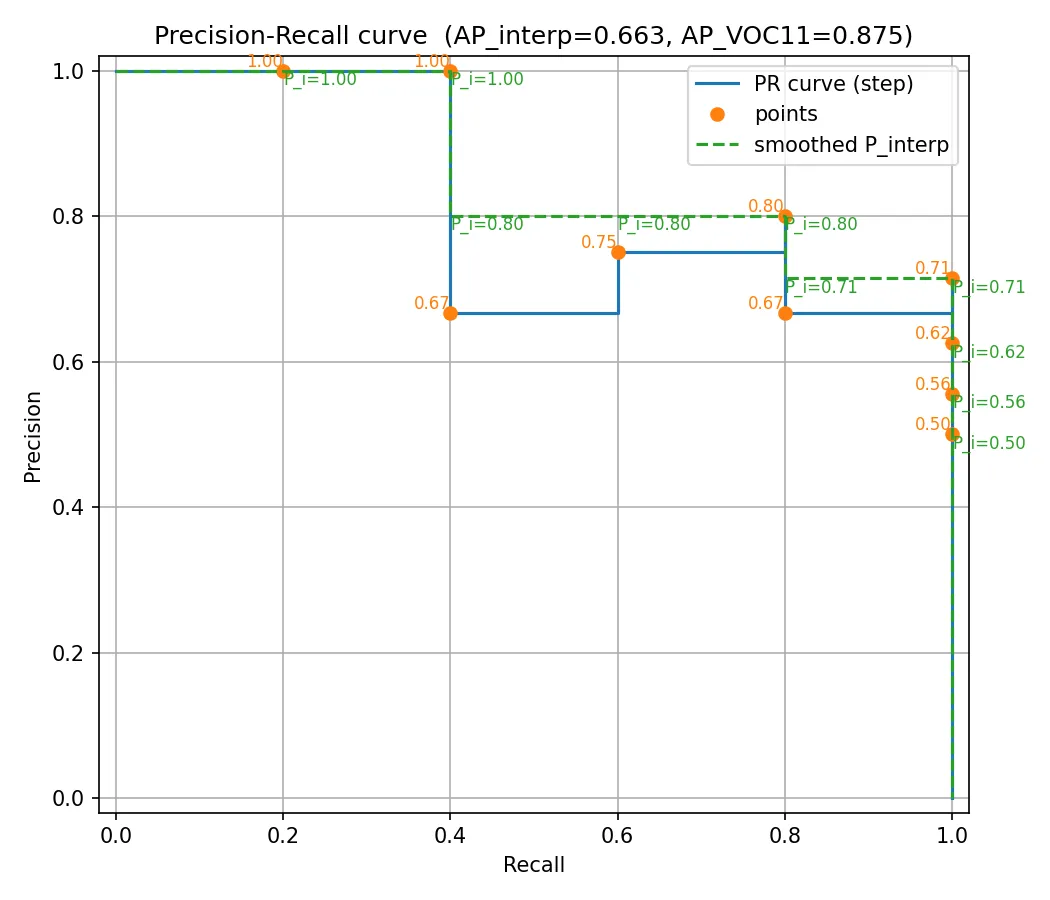
alt text

3. COCO mAP

生成：Gemini 2.5 pro

COCO mAP 采用 101 点插值法：它在召回率 [0, 0.01, 0.02, …, 1.0] 这101个点上进行采样，然后求平均。

同时，COCO mAP 不只使用单一的 IoU 阈值，而是考察模型在一系列不同严格程度的 IoU 阈值下的综合表现。其中AP@[.50:.05:.95]：是 COCO 的主要评估指标，，其中：

  • .50 表示起始 IoU 阈值是 0.5，
  • .05 表示步长是 0.05，
  • .95 表示结束 IoU 阈值是 0.95。

这个指标的计算过程如下：

  1. 在 IoU 阈值为 0.5 的情况下，计算出模型的 mAP 值。我们称之为 mAP@0.5。
  2. 将 IoU 阈值提高到 0.55，重新计算一遍，得到 mAP@0.55。
  3. 接着计算 mAP@0.60, mAP@0.65, mAP@0.70, mAP@0.75, mAP@0.80, mAP@0.85, mAP@0.90, mAP@0.95。
  4. 最后将这 10 个在不同 IoU 水平下得到的 mAP 值再求一个平均，得到最终的 AP@[.5:.95] 分数。

这个指标奖励那些定位更精准的模型。一个只能勉强达到 IoU=0.5 的模型，在 mAP@0.5 上可能得分不错，但在 mAP@0.75 或更高的阈值下会迅速得分归零。而一个定位非常精准的模型，能在所有 IoU 阈值下都保持较高的 AP，因此最终的平均分会很高。